From Braid-A-Grams to Braids

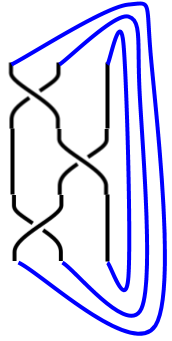
Section 1.2 From Braid-A-Grams to Braids

Objectives

Use a presentation of a group to simplify expressions and solve equations involving its generators, including groups of permutations generated by adjacent transpositions.
Use a presentation of a group, in selected cases, to determine the order of the group and orders of its element, and whether the group is abelian.

Definition 1.2.1.

A presentation of a group \(G = \langle E | R \rangle\) consists of the following data.

A set \(E=\bigl\{ a_1,a_2,\ldots, \bigr\}\) of elements of \(G\text{,}\) called generators, together with
A complete list of expressions \(R=\bigl\{ f_1(a_1,a_2,\ldots), f_2(a_1,a_2,\ldots,), \ldots \bigr\}\text{,}\) called relations, which all simplify to the identity of \(G\text{:}\)

\begin{align*} f_1\bigl(a_1,a_2,\ldots\bigr) &= e \\ f_2\bigl(a_1,a_2,\ldots\bigr) &= e \\ \vdots & \end{align*}

If the set of generators \(E\) is a finite set, we say that \(G\) is a finitely generated group. If both \(E\) and the set of relations \(R\) is a finite set, we say that \(G\) is a finitely presented group.

Example 1.2.2. Presentations of the "Four Fours".

How can we write presentations of the order-four groups in Worksheet 1.1.2?

Thinking first of the group \(G_1={1,-1,i,-i}\) we might observe that every element in this group is equal to a power of \(i\text{:}\)

\begin{align*} i^1 &= i\\ i^2 &= -1\\ i^3 &= -i\\ i^4 &= 1 && \text{(the identity)} \end{align*}

So we may take \(\{i\}\) as a complete set of generators, and the single relation \(\{i^4\}\text{,}\) and write

\begin{equation*} G_1 = \langle i \; | \; i^4 =1 \rangle\text{.} \end{equation*}

Check for yourself that

\begin{align*} G_2 = \langle 2 \; | \; 2^4 = 1 \rangle\\ G_4 = \left\langle \left[\begin{array}{rr}0&-1\\1&0\end{array}\right] \; \biggl| \; \left[\begin{array}{rr}0&-1\\1&0\end{array}\right]^4 = \left[\begin{array}{rr}1&0\\0&1\end{array}\right] \right\rangle \end{align*}

are also presentations of those groups as well.

How many generators are necessary to express \(G_3\text{?}\) How many relations?

Definition 1.2.3.

A group \(G\) whose set of generators is a single element (\(G = \{g\}\)) is called a cyclic group.

Definition 1.2.4.

A group \(G\) whose set of relations is the empty set (\(R = \emptyset\)) is called a free group.

Example 1.2.5. The Integers are a Free Group.

When addition is the operation on the set \(\mathbb{Z}\) of integers, find an example of a generator \(n\in\mathbb{Z}\) that proves

\begin{equation*} \mathbb{Z}=\bigl\langle n \; | \; \emptyset \bigr\rangle \end{equation*}

is a (cyclic) free group.

Is your \(n\) the only example possible?

In Worksheet 1.1.3 and Worksheet 1.1.4 we discovered how all anagrams, which are mere rearrangements of a finite set of letters of a word, can be “built” from a simpler set of neighboring letter swaps by drawing their braid-a-gram diagram. Moreover, there was in general more than one different braid-a-gram that could be drawn for a given anagram... but those differences can be reduced to three facts about neighboring swaps.

Every neighboring swap “undoes” itself,
Two swaps commute (their order doesn't matter) when they are disjoint, and
Two adjacent neighboring swaps (which share one strand) interact in a specific way.

As it happens, these insights about how anagrams can be built can be proven to be a complete set. In other words, any finitely presented group whose generators satisfy the same relations as (1) through (3) above is guaranteed to have an identical algebraic structure to the group of anagrams, i.e., the group of permutations with the operation of composition. That's the content of the following theorem.

Theorem 1.2.6. A Presentation of Permutation Groups.

Let \(S_n\text{,}\) with \(n\geq 2\text{,}\) be the group of all permutations of \(n\) elements.

The set of adjacent transpositions

\begin{equation*} \bigl\{\sigma_i\bigr\}_{i=1}^{n-1} = \bigl\{ (12), (23),\ldots,(n-1\; n)\bigr\} \end{equation*}

generate the group \(S_n\text{,}\) together with the relations

\begin{align} \sigma_i^2 & = () && \text{for all } 1 \leq i \leq n-1\label{eq_involution}\tag{1.2.1}\\ \sigma_i\sigma_j\, \sigma_i^{-1}\sigma_j^{-1} & = () && \text{for all } |i-j| \geq 2\label{eq_disjointcommute}\tag{1.2.2}\\ \sigma_i \sigma_{i+1}\sigma_i \sigma_{i+1}^{-1} \sigma_i^{-1}\sigma_{i+1}^{-1} & = () && \text{for all } 1 \leq i \leq n-2.\label{eq_skein}\tag{1.2.3} \end{align}

This way of viewing the permutation groups is known as the Coxeter presentation.

The three types of relation may be thought of as conveying information we learned about the “adjacent swaps” when we studied anagrams in Section 1.1, namely,

(1.2.1) says “every swap has order 2” (is its own inverse),
(1.2.2) says “swaps commute when they don't share a strand”, i.e., as long as \(i\) and \(j\) are not neighboring integers, \(\sigma_i\sigma_j = \sigma_j\sigma_i\text{,}\) and
(1.2.3) says “neighboring swaps do not commute”, but they do interact in this specific way, for example,

\begin{equation*} \sigma_1\sigma_2\sigma_1 = (12)(23)(12) = (23)(12)(23) = \sigma_2\sigma_1\sigma_2. \end{equation*}

Definition 1.2.7.

Let \(G = \bigl\langle E \; | \; R \bigr\rangle\) be a presentation of a group, and denote by \(E=\{a_1,a_2,\ldots\}\) its generators.

The word problem in \(G\) refers to the problem of determining, given two expressions in the generators (“words”) \(w_1(a_1,a_2,\ldots)\) and \(w_2(a_1,a_2,\ldots)\text{,}\) whether both represent the same group element, i.e. whether it's true that

\begin{equation*} w_1(a_1,a_2,\ldots) \stackrel{?}= w_2(a_1,a_2,\ldots). \end{equation*}

Equivalently, by Theorem 1.1.5, the word problem in \(G\) may also refer to the problem of determining, given a single word \(w(a_1,a_2,\ldots)\text{,}\) whether the element it represents is the identity:

\begin{equation*} w(a_1,a_2,\ldots) \stackrel{?}= e \end{equation*}

Happily for students but unhappily for the field of study, given a presentation for a group, the word problem in that group is unsolvable in general. In other words, there is not a recipe that's powerful enough to determine, in general, whether two words in a group are equal, or whether any given word is equal to the identity. Yet, in some cases it is possible for us to solve these word problems when the list of generators and relations is small and friendly enough.

Worksheet 1.2.1 Word Problems for Braid-a-Grams and Braids

1.

Create a “braid-a-gram” sketch of the anagram \(EAT \to TEA\) in two different ways:

Using \(\sigma_2=(23)\) as the first transposition from the top, and
Using \(\sigma_1=(12)\) as the first transposition from the top.

Write out the word in \(S_3 = \langle \sigma_1,\sigma_2 \; | \; R\rangle\) that each braid-a-gram represents.

Hint

The word beginning with \(\sigma_2\) is probably shorter than the word beginning with \(\sigma_1\text{.}\)

2.

Show how the braid-a-gram relations (1.2.1), (1.2.2), and (1.2.3) can be used to simplify one of your expressions from the previous problem into the other.

3.

Make a conjecture: Did you need all three of the relations (1.2.1), (1.2.2), and (1.2.3) to solve the word problem in the previous question? Why or why not?

4.

Create a “braid-a-gram” sketch for the anagram \(LADIES \to SAILED\text{,}\) and write out the word in \(S_6 = \langle \sigma_1,\sigma_2,\ldots,\sigma_5 \; | \; R\rangle\) that your braid-a-gram represents.

5.

Share your answer to the previous question with a classmate. If your answers are different, try to use the braid-a-gram relations (1.2.1), (1.2.2), and (1.2.3) to resolve the differences by simplifying one of your answers into the other.

Up to this point, all our “braid-a-grams” have been drawn without regard to which strand crosses over which strand at each crossing. When we wish to study knots and links from a mathematical perspective later, those overs and unders will matter! Can we make them matter now?

6.

Repeat Worksheet Exercise 1.2.1.1, but this time, sketch your diagram so that at each crossing, the strand that crosses from northwest-to-southeast crosses over the strand crossing from northeast-to-southwest. We will call these positive crossings.

Figure 1.2.8. A positive crossing and a negative crossing, respectively. The positive crossings will be represented by the generators \(\sigma_i\text{.}\)

7.

A braid which is constructed using only positive crossings is called a positive braid.

Are the two positive braids you constructed in the previous problem equal? How can you tell? (Try using physical strings to decide!)

8.

What happens when you try to repeat the steps you used in Worksheet Exercise 1.2.1.2 to turn one of your positive braid words into the other?

9.

Make a conjecture: Which of the “braid-a-gram” relations (1.2.1), (1.2.2), and (1.2.3) are still true for positive braids? Which are no longer true? Why?

For those that remain true, sketch diagrams of positive braids that suggest why they are still true.

For those that are no longer true, suggest how they may be modified.

10.

The closure of a braid is formed by joining its top endpoints with its bottom endpoints in the same position.

Figure 1.2.9. The braid \(\sigma_1 \sigma_2\sigma_1\) (in black) and its closure (includes the blue connections).

Form the closures of both of your positive braids from Worksheet Exercise 1.2.1.6. Each one is a knot. Are they the same knot? How can you tell?