Skip to main content

Section 2.1 The Rational Tangle Dance

The braids that we encountered in Chapter 1 can give rise to a great variety of knots -- indeed, to all (tame) knots and links, if we believe the final theorem of that chapter. However, the algebraic structure of braid groups is quite challenging to grapple with in general, particularly as the number of strands grows larger. In this chapter, we turn to a different construction, inspired by a braid on only two strands, but which may be twisted in two orthogonal directions. The presence of contrasting “vertical” and “horizontal” twists gives the two strands in this construction formidable power to construct a wide variety of knots, and the relative simplicity of the small number of strands gives rise to a simple invariant for these structures. Indeed, as we'll see by the end of this chapter, a single rational number is enough to provide us with a complete recipe for constructing a rational tangle, and vice versa.

Definition 2.1.1.

A rational tangle is any arrangement of two strands, whose endpoints are fixed at neighboring, disjoint vertices of a square, and which can be created through the processes listed below.

  1. Each rational tangle begins as an empty tangle, denoted \(E\text{,}\) in which the strands are horizontal, untwisted, and parallel.

  2. A twist, denoted \(T\) may be added to any rational tangle by detaching and swapping the northeastern and southeastern vertices, passing the former over the latter.

  3. A rotation, denoted \(R\text{,}\) may be performed on a rational tangle by rotating the entire tangle one-quarter turn clockwise.

Rational tangles' physical, geometrical construction lends itself well to hands-on activities. The activities in this section are typically done with four willing volunteers in a classroom, holding the ends of long ropes, but a desktop-scale kit of wires or laces can be a substitute.

Worksheet 2.1.1 The Dance Begins

For this activity, you will need two strands, such as ropes, wires, or shoelaces, of the same color. You'll also need a small envelope, with its corners cut off.

Begin by creating an empty tangle, \(E\text{.}\)

1.

Apply a rotation to form the tangle \(R\text{.}\) What tangle move(s) could you apply to return this tangle back to empty? What does this tell you about (a) the inverse of \(R\text{?}\) (b) the order of \(R\) as a group element?

2.

Return to an empty tangle. Then, apply a twist to form the tangle \(T\text{.}\) According to Definition 2.1.1, why is it not obvious that this twist can be “un-twisted” to return it to empty? (Why doesn't the definition guarantee this?)

3.

Return to an empty tangle. Then, apply three consecutive twists to form the tangle \(T^3\text{.}\) Sketch a diagram of this tangle, taking care to differentiate “over-” from “under-” crossings in your diagram.

4.

Now, rotate your tangle from the previous question twice consecutively, to form the tangle \(T^3R^2\text{.}\) Sketch a diagram of this tangle. Can you tell from your diagram whether \(T^3R^2\) is the same as \(T^3\text{?}\) Why or why not?

For the remaining exercises, form any tangle you wish, then thread its four ends through the corners of your envelope and seal the envelope shut. Write the letter \(G\) on the front of the envelope, and on the back write \(G\) backward. Leave enough length in the strands outside the envelope to permit further twists and rotations.

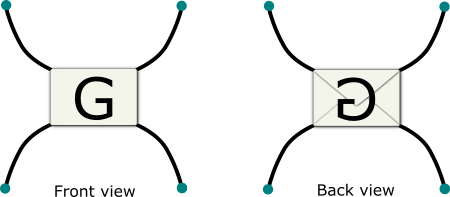
Your envelope represents an “arbitrary” rational tangle named \(G\text{.}\) Use it to respond to the following questions.

5.

Suppose \(G\) is any rational tangle, however complicated. What do you predict is the relationship between \(G\) and \(G\,R^2\) ? Can you construct an example of a tangle \(G\) that “troubles” your conjecture?

6.

Now suppose \(G\) is any rational tangle, however complicated. Add a twist to form the tangle \(G\, T\text{.}\) You wish to “cancel” (un-twist) this added twist and return to \(G\text{.}\)

  1. Which next step do you predict gets you closer to that goal: adding another twist \(T\text{?}\) Or adding a rotation \(R\text{?}\) Why?

  2. Suppose that you use a rotation \(R\) as one of your steps. Why, in light of your previous discoveries, would following with a second consecutive \(R\) probably not be the most efficient strategy to un-twist this twist?

  3. Following a strategy informed by your previous two responses, determine what series of tangle moves un-twists this added twist and returns you to the tangle \(G\text{.}\) That is, fill in this blank:

    \begin{equation*} G = G\, T\, \underbrace{\hspace{6em}}_? \end{equation*}

  4. Complete the sentence: For rational tangles, the inverse of \(T\) is \(\underline{\hspace{6em}}\text{.}\)

Worksheet 2.1.1 gives us some reassurance that rational tangles can, in fact, form an algebraic structure. Each series of tangle moves is a word built out of the tangle moves \(T\) and \(R\text{,}\) so by construction we have closure (one tangle word, followed by another tangle word, is again a tangle word). We also have an identity element, namely, the empty tangle \(E\text{.}\) And -- this is the really interesting part -- we have an inverse for each of the generators \(T\) and \(R\text{.}\) If we can “undo” each of \(T\) and \(R\text{,}\) then we can undo any rational tangle to return it to empty using the Shoes-and-socks Theorem.

However, this may not be the only strategy for determining the inverse of a tangle, as the next activity will suggest.

Worksheet 2.1.2 The Rational Tangle Dance

For this activity, you will need two strands, such as ropes, wires, or shoelaces, of the same color. You'll also need a small envelope, with its corners cut off.

Your goal in this activity is to begin from a given rational tangle, and through a series of further twists and rotations, arrive back at an empty tangle. In algebraic language, you'll be finding an expression for the inverse of each given rational tangle.

1.

Begin with an empty tangle. Form the tangle

\begin{equation*} G = T^2\, R\, T. \end{equation*}

Your tangle should look like the picture shown below.

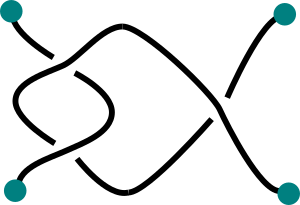
Our goal in the next three exercises will be to return this tangle to empty, by “cancelling” the factors on the right, one by one:

\begin{align*} T^2\, R\, T &= G && \text{(original tangle)} \\ T^2\, R &= G\, T^{-1} && \text{cancelling a }T \\ T^2\,&= G\, T^{-1} R^{-1} && \text{cancelling an }R \\ E &= G\, T^{-1} R^{-1} T^{-2}&& \text{cancelling a }T\text{ twice} \end{align*}
2.

Hands off your tangle for the moment. In light of your final answers to Worksheet 2.1.1, what series of steps would be necessary to un-twist the final \(T\) in this tangle? That is, what fills in the blank

\begin{equation*} T^2\,R = T^2\,R\,T\,\underbrace{\hspace{5em}}_? \end{equation*}
3.

Carry down your previous answer. What series of steps would be necessary to then cancel the rotation \(R\text{?}\) That is, what fills in the rightmost blank:

\begin{equation*} T^2 = T^2\, R\, T\, \underbrace{\hspace{5em}}_{\#2} \underbrace{\hspace{2em}}_{?} \end{equation*}
4.

Carry down your previous two answers. What series of steps would be necessary to then cancel the final two twists \(T^2\text{?}\) That is, what fills in the rightmost blank:

\begin{equation*} E = T^2\, R\, T\, \underbrace{\hspace{5em}}_{\#2} \underbrace{\hspace{2em}}_{\#3}\underbrace{\hspace{8em}}_{?} \end{equation*}
5.

Test your predictions by performing the twists and rotations shown in your answer to the previous exercise. Did you return to the empty tangle as expected?

Knowing expressions for the inverses of \(T\) and \(R\) gives you one way to determine the inverse of any rational tangle. It might, however, involve a lot more steps than are necessary, as the remainder of this activity will suggest.

6.

Begin with an empty tangle. Form the tangle

\begin{equation*} G = T^3\, R\, T^2\, R\, T^4\, R\, T. \end{equation*}

Your tangle should look like the picture shown below.

7.

Hands off your tangle for the moment. Use the strategy from the first half of this worksheet to predict a series of tangle moves that would return this tangle to empty. That is, by inverting the \(T\)'s and \(R\)'s from right to left, fill in the blank:

\begin{equation*} E = \underbrace{T^3\, R\, T^2\, R\, T^4\, R\, T}_{G} \underbrace{\hspace{12em}}_? \end{equation*}

This answer may be quite long! See if you can simplify it somewhat.

Hint

The most obvious way to simplify your answer is to replace any \(R^2\) with the empty move \(E\) (that is, to “cancel” any factor of \(R^2\)).

Solution

\(G^{-1}= RTRTRTRT^2RT^2RT^2RT^2RTRTRT^2RTRTRT^2RT^2RTR.\)

Now, seal your tangle \(G\) inside an envelope, analogously to Worksheet 2.1.1, leaving ample length outside the envelope for further twisting and rotating actions:

8.

Carefully add the following series of twists and rotations to your tangle:

\begin{equation*} R\, T^2\, R\, T^2\, R\, T^4\, R\, T^2 \end{equation*}

The tangle that results now has the notation

\begin{equation*} G\, H = \underbrace{T^3RT^2RT^4RT}_G \underbrace{RT^2RT^2RT^4RT^2}_H. \end{equation*}
9.

The inverse for \(G\) that you predicted in Worksheet Exercise 2.1.2.7 was a “word” with at least 30 letters in it. In the previous question, we're proposing an inverse for \(G\) that has a total of 14 letters (\(RTTRTTRTTTTRTT\)). Can both of these be inverses of the same rational tangle? If so, how is this possible? If not, why not?

10.

Without detaching its endpoints, cut and remove the envelope from your tangle and comb out the strands to reveal an empty tangle. Looking at the form of the tangle word \(H\) from Worksheet Exercise 2.1.2.8, do you have any conjectures about why it worked to un-tangle \(G\text{?}\)