Open Algebra and Knots: REDOAK Edition

Subsection 3.3.1 From 3-Coloration to k-Coloration

What would it mean to “extend” the number of colors available with which to color a knot diagram? We begin by reformulating tricolorability into the more general notion of \(k\)-colorability for a given value of \(k \geq 3\text{.}\) You should compare this definition with Definition 3.1.9.

The only extra mental gymnastic in this definition relative to Definition 3.1.9 is the idea that we will let the integers \(0,1,2,\ldots,(k-1)\) stand in for the “colors” of our diagram. As it turns out, this will be the key step in making colorability problems into algebraic structures.

Having established that \(k\)-colorability is a knot invariant, we turn now to the process of making \(k\)-colorability into an algebra problem. We begin with the same coloration “averaging” rule that we used to describe integer colorations of rational tangles in Section 2.2.

For a diagram having \(d\) arcs meeting at \(d\) crossings, the equations (3.3.2) form a \(d\)-by-\(d\) linear system of equations, any solution of which will give a valid \(k\)-coloration of the diagram.

In the special case \(k=3\text{,}\) the equation (3.3.2) takes a simpler form owing to the fact that \(-2\) and \(+1\) are congruent mod 3:

The following example shows how this linear system can be used to investigate the tricolorability of an 8-crossing knot, using technology to solve the resulting linear system of equations over \(\mathbb{Z}_3\text{.}\)

Exercises 3.3.1.1 Exercises

1.

The knot \(6_2\) is shown below, along with its rational tangle and its braid representations.

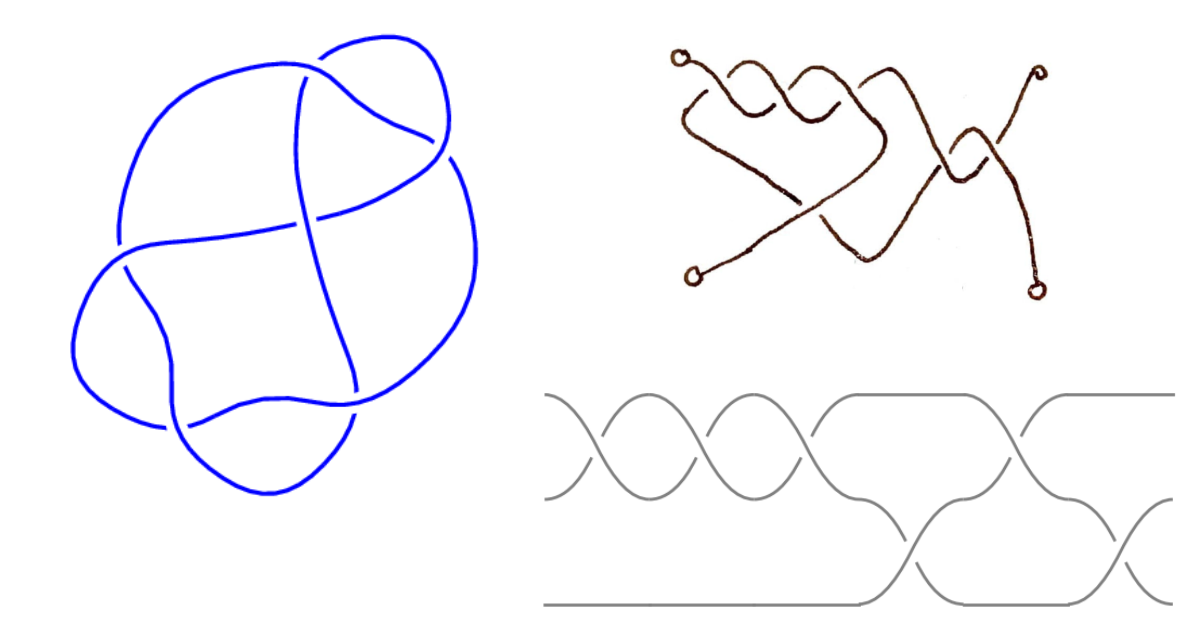
Use linear algebra to determine whether this knot is \(k\)-colorable for (a) \(k=3\text{,}\) and (b) \(k=4\text{.}\)

The Sage cell below can assist you with this calculation, once you've filled in the entries of the \(6\times 6\) matrix.

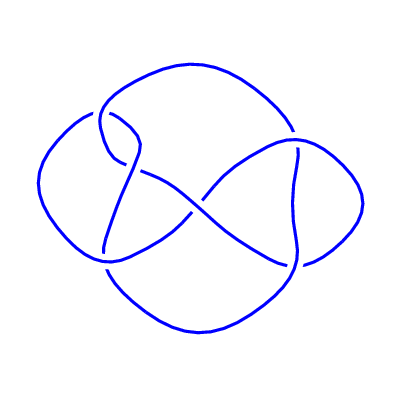
2.

Repeat the previous problem, for the diagram shown below. Discuss what your results tell you about whether this diagram might or might not be a diagram of the same knot \(K=6_2\text{.}\)

Subsection 3.3.2 One Matrix, Many Colorations

We can use the strategy of the previous section to investigate each \(k\)-colorability question for an individual value of \(k\text{.}\) This seems inefficient, however: might we be able to encode colorability information about a diagram for all possible values of \(k\) into a single algebraic object?

To get closer to this goal, we can re-envision our averaging equation (3.3.1) in a particular fashion. In place of an average, which situates the numerical value of the overstrand's color exactly halfway between the numerical values of the understrands' colors, we instead use a convex combination that permits the color of the overstrand to be some arbitrary percentage of the way along the number line segment joining the colors of the understrands.

Compare this theorem to Theorem 3.3.3, which is its special case for \(t=\frac12\text{.}\) Letting \(t\) be an indeterminate value gives us more flexibility. The matrix that results from the equations (3.3.3) is now a matrix with polynomials (\(t\)'s, \((1-t)\)'s, and \(-1\)s) in its entries.

However! One important feature that we have lost in going from the “magic average” equation (3.3.1) to the “magic convex combination” equation (3.3.3) is that the latter equation distinguishes between the two under-strands at its crossing (where in the former equation, interchanging \(x_i\) and \(x_j\) leaves the equation unchanged)! So, in order to use this new machinery, we need to give our knots an orientation, as though we're specifying in which direction we'll be driving a car along its diagram.

Definition 3.3.8. Oriented knots and crossings.

An orientation of a knot \(K\) is a choice of (normalized) direction vector along its parameterization \({\bf r}(t)\) (indicated by an arrow in any of its knot diagrams).

Given a diagram \(D\) of an oriented knot, we distinguish between its positive crossings and negative crossings according to “which direction the traffic on the bridge flows” as we drive underneath each over-strand in the direction of the orientation:

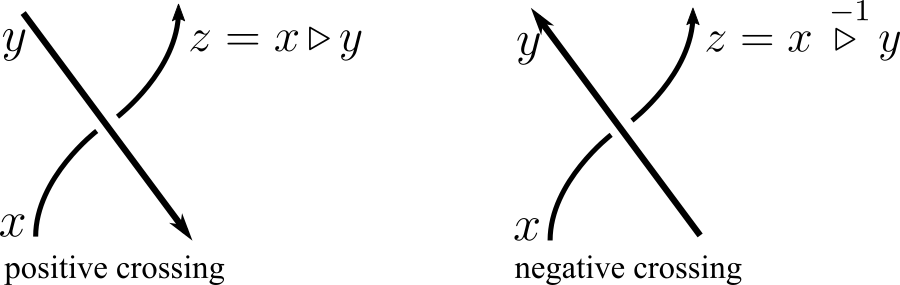
True to form, the algebra with which we tabulate a negative crossing involves an inverse of that which we use for positive crossings. In particular, a negative crossing replaces the indeterminate \(t\) with its reciprocal, \(t^{-1}\) or \(1/t\text{.}\)

We can now define a “super-structure” that encodes all the coloration information about an oriented knot, the Alexander matrix.

According to Theorem 3.3.7, then, a valid \(k\)-coloration of \(D\) corresponds to a solution of the matrix equation \(\Lambda(K) {\bf v} = {\bf 0}\text{.}\)

So, all the coloration possibilities for \(K\) can be quantified by the set of those solutions, called the null space of the matrix \(\Lambda(K)\text{.}\) Since a trivial coloration (all arcs the same color) is possible for every knot, we know that there is always a nonzero vector \({\bf v}\) that satisfies this equation:

In fact, any vector whose entries are all equal will satisfy this equation! (Coloring a diagram's arcs all red, versus coloring them all blue, correspond to different choices of the entries in this vector but both are “the same” trivial coloration.)

A testable algebraic criterion for quantifying a matrix's null space is to test its invertibility. Recall from linear algebra that a square matrix is invertible exactly when its determinant is nonzero:

Moreover, a square matrix is invertible exactly when its equations \(M{\bf x} = {\bf b}\) are guaranteed to have unique solutions. In the case where \({\bf b}={\bf 0}\) is the zero vector, this means that the null space of \(M\) is a trivial vector space:

However, we already know that our Alexander matrices \(\Lambda(K)\) have nontrivial null space, since the trivial coloration vector \((1,1,\ldots,1)\) is always a null vector. So we are guaranteed that \(\det \Lambda(K) = 0\) always; every Alexander matrix is singular (non-invertible).

So the question we can ask instead is: “how singular” is the Alexander matrix? This can be measured by the cofactors of the matrix: the determinants of the matrices which result from deleting one or more of its rows and columns.

Because the Alexander matrix is a knot invariant, all of the information we can derive from it -- including the Alexander ideals and the Alexander polynomial -- are knot invariants as well. Of these, it would seem that the one that carries the most information about the knot (because it results from crossing out the fewest rows and columns of the matrix) is the Alexander polynomial, the generator of the first Alexander ideal.

All of the above is quite a lot to swallow, so here's an example that illustrates how it works.

Shown above is a diagram of an oriented knot known as \(K=5_2\text{.}\) We'll use this diagram to compute the Alexander matrix \(\Lambda(K)\text{,}\) its Alexander ideals, and its Alexander polynomial.

First, classify each of the crossings in the diagram as positive or negative. Using the heuristic given in Definition 3.3.8, we identify that

\begin{align*} 1,2,3,4,5&&\text{ are all positive crossings. } \end{align*}

At each crossing, we select the appropriate equation (3.3.4) or (3.3.5) and substitute for \(f(x_i)\) the “incoming” under-arc, for \(f(x_j)\) the “bridge” over-arc, and for \(f(x_k)\) the “outgoing” under-arc. This gives the following five equations:

\begin{align*} t\, a + (1-t)\, d - b &=0 &\text{ (crossing 1)}\\ t\, d + (1-t)\, b - e &=0 &\text{ (crossing 2)}\\ t\, b + (1-t)\, a - c &=0 &\text{ (crossing 3)}\\ t\, e + (1-t)\, c - a &=0 &\text{ (crossing 4)}\\ t\, c + (1-t)\, e - d &=0 &\text{ (crossing 5)} \end{align*}

Arranging these in order of \(a,b,c,d,e\) we obtain a \(5\times 5\) matrix equation, the coefficient matrix of which is our Alexander matrix. (The blank entries below are zeroes.)

\begin{equation*} \Lambda(K) = \left[\begin{array}{ccc} t& -1 &&1-t&\\ &1-t&&t&-1\\ 1-t&t&-1&&\\ -1&&1-t&&t&\\ &&t&-1&1-t \end{array}\right]. \end{equation*}

If we are inclined, we can use this matrix to study the \(k\)-colorations of this diagram by choosing a value of \(t\) that's relatively prime to \(k\text{,}\) and row-reducing over the integers modulo \(k\text{.}\)

Because trivial colorations always exist, we know this matrix will have a determinant of zero. It is the determinants we obtain by first removing rows and columns of this matrix that are nonzero, and these determinants form the Alexander ideals.

First Alexander ideal: Cross out any 1 row and 1 column of this matrix, and then compute the determinant. The Sage cell below permits you to select which row/column to remove, and displays the resulting \(4\times 4\) determiniant.

Notice that in this case, the determinants are almost all exactly the same, regardless of which row/column is removed! The only difference is an overall sign.

In order to standardize these results, we agree that “the” Alexander polynomial for \(K\) is that which has been rescaled to the minimal possible (positive) degree, and which has a minimal (positive) leading coefficient. This leads to the following rescaling for this example:

\begin{equation*} -2t + 3t^2 - 2t^3 \qquad \stackrel{\times -1}\rightarrow \qquad 2t-3t^2+2t^3 \qquad \stackrel{\div t}\rightarrow \qquad 2 - 3t + 2t^2 = \Delta(K). \end{equation*}

Second Alexander ideal: Cross out any two rows and two columns of this matrix, and then compute the resulting \(3\times 3\) determinants. You'll notice there's a wider variety of polynomials in this ideal.

We can show that this ideal is generated by more than one polynomial:

\begin{equation*} \Delta_2(K) = \bigl\langle t, 1-t+t^2, (1-t)(1-t+t^2) \bigr\rangle. \end{equation*}

In principle, the second Alexander ideal might be useful for distinguishing between two knots whose first Alexander ideals (i.e., whose Alexander polynomials) are equal. But as you can imagine, this is more challenging to compute and check.

Finally, if all the \(t\) and \(1-t\) in these matrices seems like an echo of something familiar, that's because they are. The Alexander matrix \(\Lambda(K)\) for a knot encodes the same information as the Burau matrix for its associated braid (see Section 1.3).

For example, the knot \(5_2\) from Example 3.3.12 is the closure of the three-strand braid \(B=\sigma_1^3\sigma_2\sigma_1^{-1}\sigma_2\text{,}\) which has Burau matrix given by

And so by Theorem 3.3.14 its Alexander polynomial can be computed using this reduced Burau matrix:

Exercises 3.3.2.1 Exercises

1.

Compute the Alexander polynomial of the knot whose (eight-crossing) diagram is shown below.

Use your answer to predict: which prime knot among this list do you believe this is a diagram of? Can you find a series of Reidemeister moves that proves your case?