Section 3.1 A Three-Color Problem
Objectives
Sketch multiple (distinct) diagrams of a given knot, and propose “rules” for changing a diagram without changing the knot it represents.
Test by example whether given knots have a Fox tricoloration, and whether or not this depends on the diagram used for the knot.
Knots hold up the world. They're ubiquitous both for their form and function, from fashion to footwear, from boats to scouts, and wherever there are two ropes in need of cinching, knots will be there.
As the name of our course suggests, knots are the “main event” for us. In contrast to braids and tangles, knots are by far the most well-studied objects in our course, and while the floor for interesting knot questions is quite low, the ceiling is high indeed: there are many open research questions in mathematics involving knots, and knots have played crucial roles in some of the most important and far-reaching advances in low-dimensional geometry and topology research in the past twenty years. Most notably, knots were the key ingredient in Grigori Perelman's 2006 proof of the Thurston Geometrization Conjecture, which also resolved the notorious Poincare Conjecture, two of the longest-standing questions in geometry that essentially “closed the book” on classifying the shapes three-dimensional geometric objects may have.
Knots are richly studied as geometric and topological objects. For the most part, however, we will be interested in the ways in which they give rise to algebraic structures, in keeping with the theme of our exploration. We'll see over the course of this main chapter how to represent a knot as a diagram, check that a given property of diagrams is in fact a knot invariant, and discover several algebraic invariants of knots: algebraic objects or structures that capture the “knottiness” of a knot in an attempt to tell different knots apart from one another.
We begin with an agreement on what we can call a “knot”. This particular definition permits us to work with a large class of knots without worrying about bizarre infinity-driven phenomena.
Definition 3.1.2.
A (smooth) knot \(K\) is the image of a smooth, simple, closed curve \({\bf r} \colon {\mathbb R} \to {\mathbb R}^3\) in space.
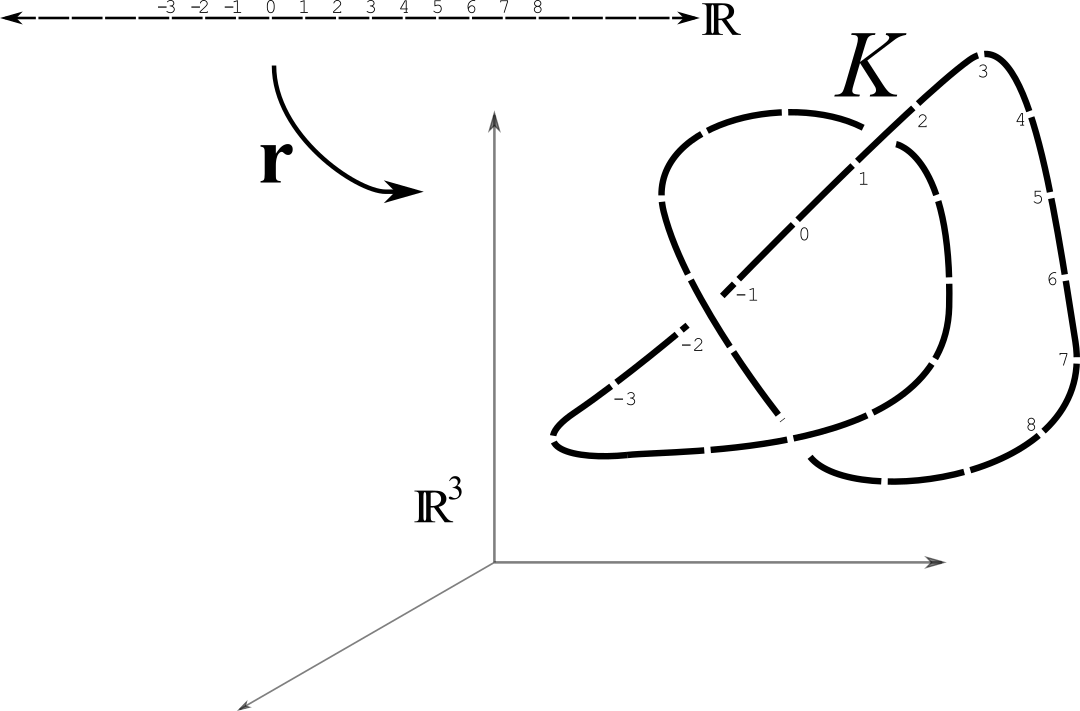
Example 3.1.4. What do those words mean?
We ultimately want to think of a knot as simply a particular type of subset of points living in space. The four words -- image, smooth, simple, and closed -- ensure that we get the kinds of subsets that “look like” knots as we intuitively and physically understand them.
Image: The image of a function is the set of all its “outputs”. This is also known as “range” in most high-school algebra contexts. We use the word image here so that we can forget about (most of) the details of the function \({\bf r}\) that parameterizes the knot as a curve, and think instead only of the points in space that the function traces out.
Smooth: A function is smooth if it is infinitely many times differentiable at all its points. In the case of a curve, this means that there is a well-defined tangent vector to our curve at each of its points, that those tangent vectors also vary continuously from point to point, that their variations also vary continuously from point to point, and so on. This is the condition that rules out so-called wild knots.
-
Closed: A curve is closed if the function \({\bf r}\colon \mathbb{R}\to\mathbb{R}^3\) is periodic, that is, if there exists a positive real number \(T\) for which,
\begin{equation*} \text{for all }t\in \mathbb{R}, \qquad \text{we have } {\bf r}\bigl(t+T\bigr) = {\bf r}(t). \end{equation*}The smallest such \(T\) is called the period of the function \({\bf r}\text{,}\) and we think of a closed curve as one whose “starting point” and “ending point” are the same, \({\bf r}(0) = {\bf r}(T).\)
Simple: A closed curve is simple if it does not intersect itself except at its starting/ending point. In other words, we cannot have \({\bf r}(t_1) = {\bf r}(t_2)\) unless \(t_1-t_2\) is a multiple of the period \(T\text{.}\) Another way to say this is to require that the function \({\bf r}:[0,T) \to \mathbb{R}^3\) to be one-to-one, i.e., require that every pair of different “times” \(0 \leq t_1 \lt t_2 \lt T\) find the curve at different points, \({\bf r}(t_1) \neq {\bf r}(t_2).\)
The main feature that you'll notice differentiates mathematical knots from everyday knots in the physical world is that mathematical knots are “closed”: to model one using a physical string, we ultimately will need to connect the string's two ends together to close the curve.
Worksheet 3.1.1 Through a Diagram, Darkly
A knot diagram (or, simply, “diagram”) is a two-dimensional sketch of a 3-dimensional knot. Diagrams consist of a set of unbroken curves called arcs, of which no more than two at a time meet at crossings, where we are careful to denote which arc is positioned “over” (i.e., nearer the viewer) than the other.

Simple, right? What's less simple is the fact that we can view a given knot from infinitely many different perspectives in space, and different perspectives can give different-looking diagrams. We'll begin by exploring how diagrams may differ while the knot remains the same.
1.
Using either a physical version, or by rotating the virtual version, of the knot \(K(3,2)\) from Figure 3.1.5, find a diagram of this knot having exactly 4 crossings. Sketch it on a blank sheet, and label it “\(D_4\)”.
2.
Explain to someone who doesn't have a physical or virtual copy of this knot: How could the diagram \(D_4\) be (easily) obtained from \(D_3\text{?}\)
How does this result compare to your answers to Worksheet Exercise 1.1.4.2?
3.
Using the results of the previous two problems, conjecture a statement that could fill in this blank:
Given any knot \(K\) and a diagram \(D\) of \(K\text{,}\) we can always obtain a new diagram \(D'\) of the same knot, having exactly one more crossing than \(D\text{,}\) by...
We'll call this our first rule of diagrams.
4.
Using either a physical version, or by rotating the virtual version, of the knot \(K(3,2)\) from Figure 3.1.5, find a diagram of this knot having exactly 5 crossings. Sketch it on a blank sheet, and label it “\(D_5\)”.
5.
Explain to someone who doesn't have a physical or virtual copy of this knot: How could the diagram \(D_5\) be (easily) obtained from \(D_3\text{?}\)
How does this result compare to your answers to Worksheet Exercise 1.1.4.2?
6.
Using the results of the previous two problems, conjecture a statement that could fill in this blank:
Given any knot \(K\) and a diagram \(D\) of \(K\text{,}\) we can always obtain a new diagram \(D''\) of the same knot, having exactly two more crossings than \(D\text{,}\) by...
We'll call this our second rule of diagrams.
7.
Figure 3.1.7 shows a part of a diagram of a knot, “zoomed-in” on three of its crossings. Adjusting the slider moves the location of the bottommost (grey) arc in this diagram.
Sketch two different three-crossing diagrams that can be obtained from adjusting the figure above.
Explain: All else being equal, how do we know that the changes between these two diagrams do not change the underlying knot being represented?
8.
Using the results of this problem, conjecture a statement that could fill in this blank:
Given any knot \(K\) and a diagram \(D\) of \(K\text{,}\) we can always obtain a new diagram \(D'''\) of the same knot, having exactly as many crossings as \(D\text{,}\) by...
We'll call this our third rule of diagrams.
9.
Finally, begin from the original diagram \(D_3\) again, and find a diagram of the same knot that has a total of exactly 6 crossings. Sketch it, and label it “\(D_6\)”.
Does this give rise to a new rule of diagrams? Or can you obtain it by using the first, second, and third rules you discovered above? How can you tell?
Knot diagrams will be our primary tool both for representing knots, and for doing computations and algebra with knots. Our desire to do both leads us directly to a challenge: when we use a diagram of a knot to attempt to understand one of the knot's properties, how do we know that that property is actually seeing the knot, and not seeing the diagram?
In other words, since the same knot can have (infinitely!) many different diagrams, how can we be certain that we're seeing a property that transcends diagrams and actually tells us something about the knot itself, regardless which diagram we've chosen to represent it?
How can we be sure not to judge a knot by its cover? By studying its “invariant” properties, according to this definition.
Definition 3.1.8.
Let \(K\) be a knot. A logical property \(P\) is called a knot invariant if, for all pairs of diagrams \(D,D'\) of \(K\text{,}\) we have
In other words, property \(P\) is a knot invariant if it is either true for every possible diagram of \(K\text{,}\) or false for every possible diagram of \(K\text{.}\)
Every knot invariant has the power of discrimination: Given two diagrams \(D_1,D_2\) and a knot invariant \(P\text{,}\) if \(P\) is true for one diagram and false for the other, then we know for certain that those diagrams represent different knots. However, most knot invariants do not have the power of confirmation: We cannot always say that if \(P\) is true for both diagrams, then those diagrams represent the same knot. An invariant that does that, if one exists, is called a complete invariant. Those are the “holy grail” of knot theory, since they would completely classify all types of knots -- in the same way that the fraction of a rational tangle classified all rational tangles (Section 2.2).
We will return to invariants in more generality in the next section. For now, let's use the results of Worksheet 3.1.1 to explore one example of an invariant, called tricolorability.
Worksheet 3.1.2 Three Colors Shining Through
in this activity we'll solve some discrimination problems using a knot invariant called tricolorability.
Definition 3.1.9.
Let \(K\) be a knot, and \(D\) be one of its diagrams. A 3-coloring of \(D\) is a function
which assigns one of the three colors red, green, or blue to each arc of the diagram.
A 3-coloring of \(D\) is called a valid 3-coloring if each crossing of \(D\) is one of the following:
...a meeting of three arcs of the same color, or
...a meeting of three arcs of three different colors.
A diagram \(D\) is called (Fox) tricolorable if there exists a valid 3-coloring of \(D\) besides the “trivial” example (all arcs the same color).
We've been careful in this definition to paint tricolorable as a property of diagrams rather than a property of the knots behind those diagrams. Let us investigate whether, indeed, the question of tricolorability depends on the diagram chosen for a given knot.
1.
Shown below is a diagram of the knot \(K(3,2)\) with a valid coloration. However, as shown it does not prove that this diagram is tricolorable (why not?).
By clicking on the arcs to recolor them, show that this diagram is, in fact, tricolorable.
2.
Use a sketch of your diagram \(D_4\) from Worksheet Exercise 3.1.1.2 to determine whether \(D_4\) is tricolorable. (Remember, this is also a diagram of the same knot \(K(3,2)\text{.}\))
Then, complete this sentence with a conjecture: When the first rule of diagrams is used to add a crossing to a tricolorable diagram, we know that...
3.
Use a sketch of your diagram \(D_5\) from Worksheet Exercise 3.1.1.4 to determine whether \(D_5\) is tricolorable. (Remember, this is also a diagram of the same knot \(K(3,2)\text{.}\))
Then, complete this sentence with a conjecture: When the second rule of diagrams is used to add two crossings to a tricolorable diagram, we know that...
For the remaining questions, we will assume that tricolorability is indeed a knot invariant.
4.
True, False, or Cannot Decide: Is the diagram shown below also a diagram of the knot \(K(3,2)\text{?}\) Justify your answer.
5.
True, False, or Cannot Decide: Is the diagram shown below also a diagram of the knot \(K(3,2)\text{?}\) Justify your answer.
Finally, we close with an example of what happens when we build more complex knots out of simpler ones.
Definition 3.1.13.
Let \(K_1,K_2\) be two knots. The connected sum of \(K_1\) and \(K_2\) is a knot formed by cutting one strand of each knot, away from its crossings, and attaching them to one another.
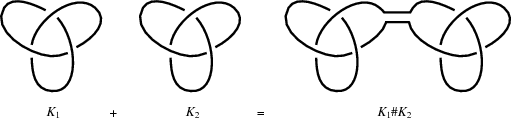
https://mathworld.wolfram.com/KnotSum.html6.
Give a convincing justification (a proof, even) for the following theorem. Let \(K_1,K_2\) be two knots. If \(K_1\) is tricolorable, then the connected sum \(K_1 \# K_2\) is tricolorable.
Theorem 3.1.15.
See if your strategy for coloring the knot in Worksheet Exercise 3.1.2.5 gives you any clues. If not, try coloring it in a different way than before.