Section 1.1 Anagram Algebra
Objectives
- Discover the algebraic nature of word anagrams.
- Discuss the necessity of the three properties of an algebraic group for algebraic reasoning.
- Use the definitions of the order of a group and the order of an element in a group.
- Use cycle notation to denote and perform computations with permutations.
- Use a Cayley table to depict the structure of an algebraic group.
- Uncover a connection between permutations and a type of braids.
What is algebra, and where (else) can we find it? Ask a high-school student this question. Then, ask a research mathematician. You may get two very different answers. 

The goal of this introductory set of activities is to broaden our horizons to the meaning of the word “algebra”, so that we will be able to recognize algebraic structure and algebraic reasoning in unfamiliar and unexpected contexts. We'll begin from simple anagram puzzles, and end with some fundamental understandings of the raw ingredients necessary for algebra.
Worksheet 1.1.1 Four- and Five-Letter Anagrams
An anagram is a rearrangement of the letters in a word. Usually, anagrammers care about those rearrangements that also form an intelligible word, such as the rearrangement of \(INTEGRALS\) into \(GNARLIEST\text{.}\) Mathematically, we may also permit rearrangements that are nonsensical, such as \(GRISTLENS\text{.}\)
For simplicity, let's think about anagrams of words in which all letters are different. We don't want to worry about whether the “E”'s have been transposed when \(PEEK\) turns into \(KEEP\text{,}\) for example.
1.
Find at least two anagrams of the word \(TIME\) that are dictionary English words.
2.
Find at least two anagrams of the word \(LEAST\) that are dictionary English words.
3.
Imagine that you have to explain to a friend how to perform the anagram \(STONE \to ONSET\text{,}\) by moving one letter at a time, but without mentioning any of the letters by name. What step-by-step instructions could you give them?
4.
Refer to your answer to #3. This time, write instructions for the opposite anagram, \(ONSET \to STONE\text{.}\) How are they similar to the original? Different?
5.
Refer to your answer to #3. What happens if you apply your original \(STONE \to ONSET\) instructions, but using the word \(ONSET\) as the beginning word instead?
6.
Repeat the previous three exercises, using the anagram \(SHALE \to LEASH\text{.}\) What's different this time around?
7.
In each of the following pairs of anagrams, which would you say is “more complicated” and why? Or are they equally complicated? Can you mathematize your intuition in some way?
\(SPARE \to SPEAR\) or \(SPARE \to PARSE\text{?}\)
\(SIREN \to RINSE\) or \(SIREN \to RESIN\text{?}\)
\(WORDY \to ROWDY\) or \(WORDY \to DOWRY\text{?}\)
8.
How many anagrams does the word \(RISE\) have, if we include those that are not dictionary English words? What about \(CATER\text{?}\) Where in the high-school math curriculum is the “shortcut” formula taught that addresses this question?
The heart of Worksheet 1.1.1 is the explanations you provided in #3-5 and then again in #6. Here, you first described a process, namely, that turns one five-letter word into a different five-letter word. Then, you supplied another description for the opposite of that process. Finally, you investigated the result of composing that process with itself, that is, following it twice in succession.
Now, consider what we do in our first algebra lessons in middle- and high-school. We begin with a numerical quantity (say, \(2\)). We apply a process, for example, by adding seven (\(2 + 7\)). We understand that that process can be reversed: it has an opposite, that we call subtracting seven (\(2 + 7 - 7\)), and we know this is the opposite because \(2 + 7 - 7\) is the same as, simply, the original expression \(2\text{.}\) And, we know that this process can be repeated, followed up by itself, forming expressions like \(2 + 7 + 7\text{.}\)
What we mean by “algebra” lies in the commonalities between the previous two structures. We are engaging in algebraic reasoning any time we describe combinable, reversible processes. Using traditional algebra notation, we need our processes to combinable because in order to simplify the left-hand side of the equation
we need to know that the objects “\(X\)” and “\(Y\)” can indeed be combined together by the process “\(+\)” into a single object of the same type, “\(Z\)”. And, in order to solve this equation for \(X\text{,}\) say, we need the operation to be reversible: we need to have an opposite procedure “\(-Y\)” that we can apply on both sides to obtain
So it is that the two horsemen of high-school algebra, simplify and solve, necessitate the three types of structure that we will say characterizes all kinds of algebraic reasoning: combine-ability, reversibility, and “neutrality”, the latter being the ability of the “zero” in the above calculation to disappear. This brings us to our first definition.
Definition 1.1.3. Group.
Let \(X\) be a set, and let \(\cdot\) be a binary operation on \(X\text{,}\) that is, a function which inputs two elements \(x,y \in X\) and outputs an expression \(x\cdot y\text{.}\)
We say that \(G = \bigl( X, \cdot \bigr)\) is a group if four conditions are satisfied:
(Closure.) For all \(x,y \in X\text{,}\) we have \(x\cdot y \in X\text{.}\)
(Identity.) There exists an element \(e \in X\) for which, for all \(x \in X\text{,}\) we have \(e\cdot x = x\) and \(x \cdot e = x\text{.}\)
(Inverses.) For all \(x\in X\text{,}\) there exists an \(a\in X\) such that \(x\cdot a = e\) and \(a\cdot x = e\text{.}\)
(Associative law.) For all \(x,y,z \in X\text{,}\) we have \(x \cdot (y\cdot z) = (x\cdot y) \cdot z.\)
When \(G = \bigl(X,\cdot\bigr)\) is a group, we call \(X\) the set of elements of \(G\) and we call \(\cdot\) the operation of \(G\text{.}\)
The associative law, which makes its first appearance in this definition, is a convenience that permits us to do things like raise an element to an integer power, e.g., \(g^5 = g\cdot g\cdot g\cdot g\cdot g\text{,}\) without worrying about which “\(g\cdot g\)” in that product is meant to be evaluated first.
It is perhaps surprising that, given this relatively sparse set of requirements for a group, there are nevertheless many important properties that can be deduced from them.
Theorem 1.1.4.
Let \(G=(X,\cdot)\) be a group. Each of the following holds.
(Identity is unique.) There is exactly one element \(e \in X\) satisfying, for all \(x\in X\text{,}\) the equation \(x\cdot e = x = e\cdot x\text{.}\)
(Inverses are unique.) For all \(x\in X\text{,}\) there is exactly one element \(a\in X\) for which \(x\cdot a = e = a\cdot x\text{.}\)
-
(Cancellation property.) For all \(x,y,z \in X\text{,}\) we have
\begin{gather} \text{If } x\cdot y= x \cdot z, \text{ or if } y \cdot x = z\cdot x, \text{ then we must have } y = z.\label{eq_cancellation}\tag{1.1.1} \end{gather}
Because of #1-2 above, we may speak of “the” identity element of a group, and “the” inverse of any element \(x\text{,}\) which we denote \(x^{-1}\text{.}\)
Video proof.
Theorem 1.1.5. Shoes-and-socks.
Let \(G=(X,\cdot)\) be a group, and \(g,h\in X\) be two elements.
The inverse of the element \((g\cdot h)\) is the composition of the inverses of \(g\) and \(h\text{,}\) in the opposite order:
Video proof.
Conspicuous by its absence is the “commutative law.” This is not an accidental omission, but rather a special property that some groups enjoy but many (most?) do not. A group \(G = (X,\cdot)\) is called an abelian group if it also satisfies the commutative law:
Definition 1.1.6.
Example 1.1.7. Video: Some examples of groups.
Here are a few example groups. Note that all of these groups also enjoy the commutative law, that is, they are abelian groups.
Eventually, when the context is clear, we will use simpler notation \(G\) to denote an arbitrary group rather than listing its elements and operations \(G=(X,\cdot)\text{.}\)
Definition 1.1.8.
A group \(G=(X,\cdot)\) is called a finite group if its set of elements \(X\) is a finite set. In this case, if \(X\) has \(n\) elements, we say that the order of the group is \(n\text{,}\) and write
A group which is not finite is called an infinite group, and we write \(\bigl|G\bigr| = \infty.\)
When \(G\) is a finite group, it is possible to explicitly write down a list of all its elements, and every pairwise product of those elements. This information can be arranged in abstract algebra's equivalent of a multiplication table, known as an “operation table” or Cayley table.
Example 1.1.9. Video: Cayley table examples.
Worksheet 1.1.2 The Four Fours, Group Theory Version
Listed below are four groups, each of order four. Construct a Cayley table for each, and address the questions listed below.
1.
How can you tell from your Cayley table that each of the four group axioms is satisfied? (What would happen in the Cayley table if an axiom were violated?) Determine the identity element of your group, and at least one interesting pair of an element and its inverse.
2.
Which one of these Cayley tables doesn't belong with the others? Why? Try to look past any superficial differences!
3.
What instructions could you give a middle-school math student for determining whether two Cayley tables represent “the same” abstract structure?
Since the associative law makes the expression unambiguous, we can evaluate any integer power of a group element:
Checkpoint 1.1.10. Familiar exponent properties still hold.
Use the above definition to convince yourself that, for any group element \(g\text{,}\) we have:
For all integers \(k,\ell\in\mathbb{Z}\) we have \(g^k\cdot g^{\ell} = g^{k+\ell}.\)
As a result, we must have \(g^0 = e\text{,}\) the identity element of the group. (Hint: Choose an arbitrary integer \(k\) and rewrite \(0 = k + (-k).\))
This permits us to define another meaning of the word “order”, this time as it applies to an element of a group.
Definition 1.1.11.
Let \(G = \bigl(X,\cdot\bigr)\) be a group and \(g\in X\) be an element. The order of \(g\) in \(G\) is the least positive integer \(k\) for which \(g^k = e\text{.}\)
When such an integer exists, we write \(\bigl|g\bigr| = k\text{.}\) Otherwise, we say that \(g\) has infinite order and may write \(\bigl|g\bigr| = \infty.\)
Checkpoint 1.1.12. Order in the “Four Fours”.
Revisit the Cayley tables from Worksheet 1.1.2, and use them to determine the order of each element in each group.
Does this reassure you of your answer to “which Cayley table doesn't belong”? Why or why not?
Let's revisit the anagrams in Worksheet 1.1.1 to conclude this section. How can we formalize the idea of anagrams being elements of a group?
We spoke of each anagram as being a “process” of rearrangement of letters, and in the activity you came up with descriptions of those rearrangements that did not call the letters by name. If each rearranging process is an element of a group, and that group's operation is to follow (compose) one process with the next, we can study rearrangements as a group.
Checkpoint 1.1.13. Anagram identity and inverse.
We would expect the anagram \(SOBER \to \underline{\hspace{5ex}}\) to represent the identity element in our group.
We would expect the anagram \(PLATE \to PLEAT\) to have the inverse element \(PLATE \to \underline{\hspace{5ex}}\text{.}\)
The operation in this group is “follow one rearrangement with another”. What rearrangement would be “invisible” (undetectable) if it followed, or was followed by, another rearrangement?
The operation in this group is “follow one rearrangement with another”. Write out step-by-step directions for the original anagram, then try following them in reverse. That way, if you were to follow your original directions, and then your reverse directions, you would end up back at the original word (you'd have the identity element, a trivial anagram), no matter which five-letter word you started with.
The “trivial” anagram, \(SOBER \to SOBER\text{.}\)
The inverse is \(PLATE \to PLTEA\text{.}\)
To study the algebra of anagrams with more ease, we define a notation for the step-by-step directions you gave. This notation is called cycle notation.
Checkpoint 1.1.14. How cycle notation works.
You can use this interactive Scratch app to explore how cycle notation works. Click to open it in a new window.
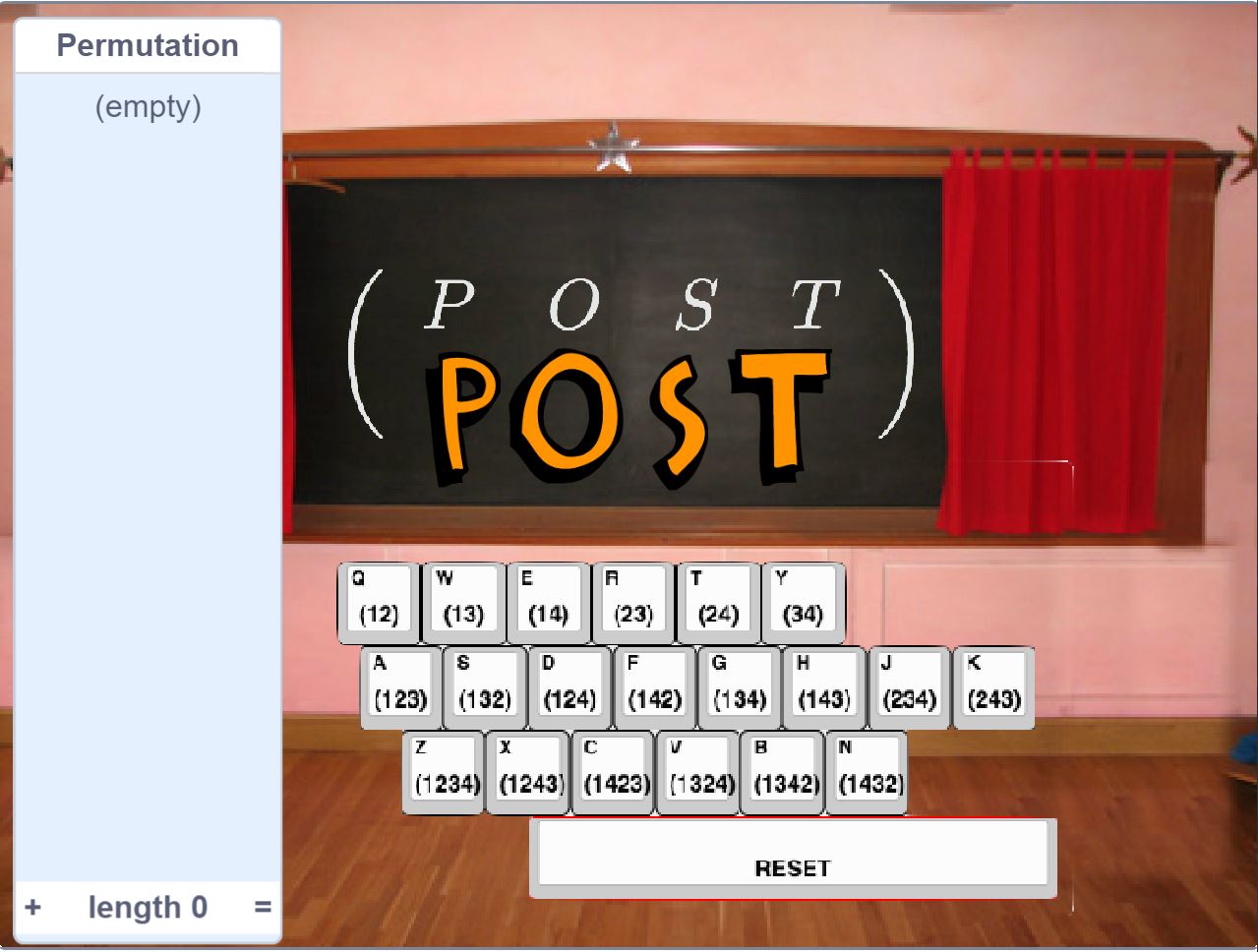
Use the app to figure out: what is the result of following the cycle \((12)\) with the cycle \((24)\text{...}\)as an anagram? ...as a single cycle from elsewhere on the "keyboard"?
Repeat the previous, but reversing the order, \((24)\) followed by \((12)\) instead. What does your result tell you about whether the groups comprised of anagrams are abelian?
What is the difference between “\((14)\) followed by \((23)\)” and “\((1423)\)”? How would you describe what each of these is doing to the four positions in the word POST?
Can you give step-by-step instructions for how to apply the cycle \((243)\) to the word \(PLEA\text{?}\)
Worksheet 1.1.3 Teasing Anagrams Apart
In the anagram \(SHALE \to LEASH\text{,}\) you noticed that two pairs of letters (positions) trade places: the first and fourth, which we may denote \(r=(14)\) in cycle notation, and the second and fifth, \(s=(25)\text{.}\)
If we treat each of these two-place swaps (called transpositions) as its own anagram, then we can study the algebraic structure formed by these anagrams in several ways.
1.
What anagram is discovered for \(SHALE\) defined by each of the following?
-
The identity \(e=()\text{:}\) \(\quad SHALE \to\underline{\hspace{5ex}}\)
The transposition \(r=(14)\text{:}\) \(\quad SHALE \to \underline{\hspace{5ex}}\)
The transposition \(s=(25)\text{:}\) \(\quad SHALE \to \underline{\hspace{5ex}}\)
The permutation \(rs=(14)(25)\text{:}\) \(\quad SHALE \to \underline{\hspace{5ex}}\)
The permutation \(sr=(25)(14)\text{:}\) \(\quad SHALE \to \underline{\hspace{5ex}}\)
The permutation \(s^2=(25)(25)\text{:}\) \(\quad SHALE \to \underline{\hspace{5ex}}\)
2.
Explain: How do we know that each of the (a) closure, (b) identity, and (c) inverses axioms of a group is satisfied by \(X=\{ e, r, s, rs \}\) with the operation of composition?
3.
Let \(G\) be the group whose elements are \(X=\{e,r,s,rs\}\) with the operation of composition. Create a Cayley table for \(G\) using these elements' names. (For fun, also create a Cayley table using their actions on the word \(SHALE\text{.}\))
4.
Refer again to the Four Fours Worksheet 1.1.2. Where does this group \(G\) belong among the four groups in that activity? How do you know?
A visual way to represent the permutation that turns \(SOBER \to ROBES\) is to arrange the words above one another, and draw a curve connecting each letter's starting position with its ending position.

You might try constructing this diagram using your loom and string.
5.
How would you express the anagram \(SOBER\to ROBES\) using cycle notation? \(u = \bigl( \qquad \qquad \bigr)\)
6.
Cover up this diagram with a piece of opaque paper. Slowly pull the paper down until you reveal the first crossing of two lines. Write the anagram and the cycle notation it corresponds to, like so:
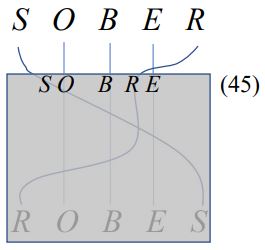
Continue, stopping after every new crossing you reveal to write both the new anagram and the transposition that occurred at that crossing, using cycle notation. Repeat until you've arrived at the final word, \(ROBES\text{.}\)
Tracing the curves back to the original word shows you the anagram. But remember that the cycle notation comes from which two positions are trading places at that moment -- so don't let the original positions of the letters throw you off!
7.
Use your answer to the previous question to predict: how can the permutation \(u\) that you found in #5 be written as a composition of adjacent (“neighboring”) transpositions?
8.
Redraw this figure (or manipulate your loom and strings) so that the topmost crossing and the bottom-most crossing both represent the same transposition \((12)\text{.}\) Use this new diagram to discover a different answer to #7.
9.
Can you redraw the figure so that the top- and bottom-most crossings are both \((45)\text{?}\) What about \((23)\text{?}\)
10.
Can you redraw the figure so that the composition of crossings is a palindrome reading the same in forward order as reverse order? How, or why not?
11.
What conjecture(s) can you make about anagrams in general, based on the results of this worksheet? Test one of your conjectures on the anagram \(STONE\to ONSET\text{.}\)
Start exploring by asking, for each of #6-9, “do I think this always works?” If you think the answer is yes, how could you phrase a general statement of which this \(SOBER\to ROBES\) example is a special case?
You can use the Sage Math worksheet below to experiment: Does changing the order in which the seven crossings are encountered in the \(SOBER \to ROBES\) anagram change the result?
Worksheet 1.1.3 gives us our first taste of how the study of algebra -- group theory, in particular, motivated at first by the study of simple anagrams of words -- can give rise to a physical object that resembles a set of tangled strings! This bodes well for the future of the relationship between algebraic structures on the one hand, and physical knots on the other. As happened in this worksheet, the crossings, those places where one string passes through another, will play a crucial role in uncovering algebraic structure from knot-like objects.
Note also that, in this example, it did not matter how one string passed through another, that is, it did not matter whether one passed over the other in three-dimensional space, or vice versa, or if somehow these incorporeal strings literally transected one another. We'll see how that makes our algebra simpler, at the cost of sacrificing a question that will become much more critical if we want to study physical knots. Indeed, we'll see in this chapter how, as soon as we care which string passes over which at a crossing, the structure we get, called a braid, has a rich algebraic life indeed.
Worksheet 1.1.4 Braid-a-Grams Wrapup
1.
Using cycle notation -- for example, \((23)\) representing the transposition of 2nd and 3rd positions -- draw a “braid-a-gram” of the given word that depicts each of the following equations.
-
Beginning from the word \(GOAL\text{,}\) show that
\begin{equation*} (23)\, (23) = (). \end{equation*} -
Beginning from the word \(BASTE\text{,}\) show that
\begin{equation*} (12)(45) = (45)(12). \end{equation*} What identity results from the following pair of equivalent braid-a-grams?
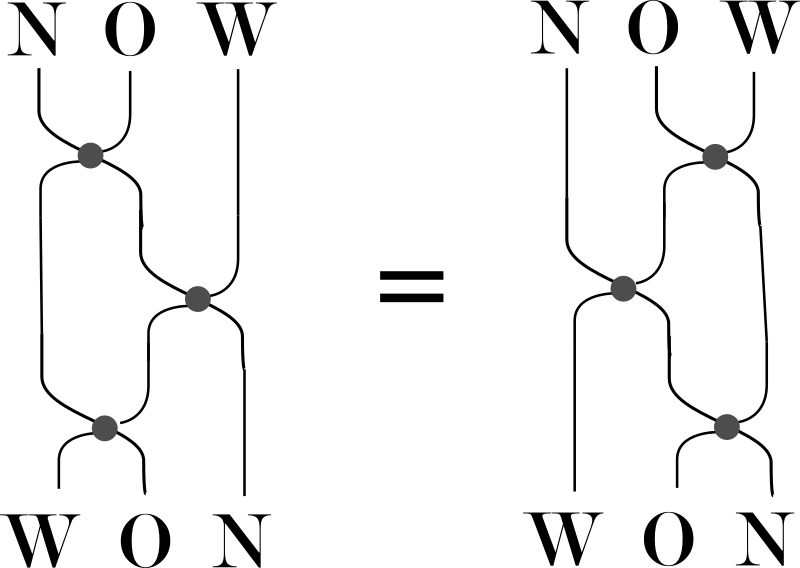
2.
Every braid-a-gram for the anagram \(SOBER \to ROBES\) must include at least 7 crossings. (Why?)
Find as simple a way as possible -- by redrawing a single strand -- to create another braid-a-gram for \(SOBER \to ROBES\) having...
...exactly 9 crossings.
...exactly 8 crossings.
The 8-crossing example is tricky. Adding a single crossing to your diagram seems impossible as soon as one strand crosses over another...