Of Cats and Combinatorics (Help!)

The older I get, the more time I wish I’d spent with combinatorics. That was true when I got tapped to teach our undergraduate combinatorics course for a semester in 2011 – there, I was rescued by the grace of a colleague and an excellent, inquiry-based text. And it’s true again now: I’ve got a counting problem in a research project that I just can’t crack. So I’m opening it up to the internet, here first and on MathOverflow later if needed.

A Simple Version

Suppose you’re a pet photographer. You have two cats, and two cat sweaters. Not every cat must wear a sweater, nor must every sweater be used. But no cat may wear more than one sweater, nor may we squeeze multiple cats into the same sweater. How many different photos are possible?

The Answer: Seven.

The Balls-and-Urns Version: We have two urns, each with two balls. All are distinguishable. We may choose no balls at all and be done. Or, if we choose a ball from the first urn (a cat) we then must choose a ball from the second urn (a sweater) with which to match it. Then, we can either quit, or continue without replacement. So if our urns are

[latex]\mathscr{C} = \{ {\rm Amber}, {\rm Bosco} \} \quad \mathscr{S}=\{ {\rm Red}, {\rm Green}\}[/latex]

the seven possible photos are:

1. No matches (neither cat wears a sweater).
2. Amber wearing Red only.
3. Amber wearing Green only.
4. Bosco wearing Red only.
5. Bosco wearing Green only.
6. Amber wearing Red, Bosco wearing Green.
7. Amber wearing Green, Bosco wearing Red.

The Grammatical Version: Represent the cats by the symbols [latex]\mathscr{C}=\{A,B\}[/latex] and the sweaters by the numbers [latex]\mathscr{S}=\{1,2\}[/latex]. Define a word as an element of the Cartesian product [latex]\mathscr{C}\times\mathscr{S}[/latex], and a sentence as a subset of the power set [latex]2^{\mathscr{C}\times\mathscr{S}}[/latex] in which no element of [latex]\mathscr{C}[/latex] nor [latex]\mathscr{S}[/latex] appears more than once.

Then among the [latex]16=2^{2\times 2}[/latex] elements in this power set, exactly seven are sentences:

1. [latex]\emptyset[/latex]
2. [latex]\{ (A,1) \}[/latex]
3. [latex]\{ (A,2) \}[/latex]
4. [latex]\{ (B,1) \}[/latex]
5. [latex]\{ (B,2) \}[/latex]
6. [latex]\{ (A,1), (B,2) \}[/latex]
7. [latex]\{ (A,2), (B,1) \}[/latex]

The Graph Theory Version: Consider the complete bipartite graph [latex]K_{2,2}[/latex]. If the first partite part represents the cats and the second the sweaters, then each edge in this graph represents a possible cat-to-sweater fitting.

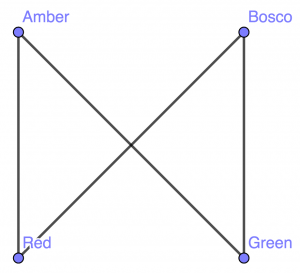
In this formalism, a “photograph” corresponds to a matching on this graph, i.e., a subset of its set of edges in which no two edges share a common vertex (because one cat can’t wear multiple sweaters, nor vice versa). The graph [latex]K_{2,2}[/latex] has a total of seven matchings, shown below.

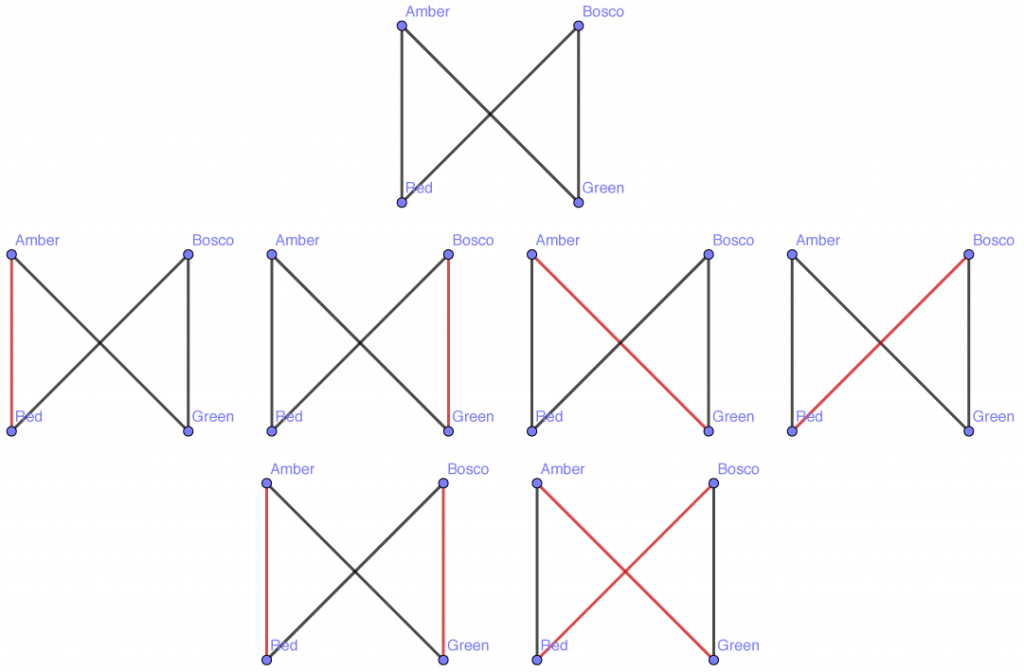
The total number of distinct matchings possible in a graph is known as its Hosoya index, or Z-index. This index has been computed for several families of graphs; for the complete bipartite graphs we have

[latex]Z(K_{m,n}) = n!\, L_n^{m-n} (-1),[/latex]

where [latex]L_n^{m-n}(x)[/latex] is the associated Laguerre polynomial. That this special function pokes its head into our problem ought to be surprising! It arises because matchings for this family of graphs satisfy identical recurrence relations to the solutions of the associated Laguerre differential equations (Godsil & Gutman 1981).

The Growing Problem

What I’m working on right now is a more general case which:

• Relates to the complete k-partite graph [latex]K_{p_1,p_2,\ldots,p_k}[/latex], directed in a natural way (all edges oriented from top to bottom, for example).
• Replaces edge set with path set. Where a matching cannot include two edges that share a vertex, I want to allow this sharing – but only in the case where the shared vertex is intermediate to a path.

For example, suppose I add a third sweater and also a set of two fabric bows to my photography example:

[latex]\mathscr{C} = \{ {\rm Amber}, {\rm Bosco} \} \quad \mathscr{S}=\{ {\rm Red}, {\rm Green}, {\rm Yellow} \} \quad \mathscr{B}=\{ {\rm Satin}, {\rm Tuille}\}[/latex]

All seven of these items need to be in our photo. In how many ways can they be combined? Now, we have a complete tripartite graph [latex]K_{2,3,2}[/latex], and each photograph is represented by a vertex-disjoint set of paths:

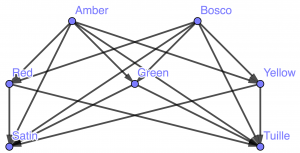
In how many different ways can we draw (any number of) paths on this graph such that no two paths share a vertex?

The answer appears to be 91. Thinking recursively, we could begin with the sum of the bipartite Hosoya indices we’d get by either dressing no cats, using no sweaters, or using no bows. (In these cases, we’re restricting to paths of length 1, i.e., edges.) Since the empty matching belongs in all three of these, we also need to subtract 2 to avoid counting it thrice.

[latex]Z(K_{3,2}) + Z(K_{2,2}) + Z(K_{2,3}) -2 = 13 + 7 + 13 -2 = 31.[/latex]

But this number misses the two-edge paths, the dapper kitties wearing a sweater and bow. If we want Amber alone to wear both sweater and bow, there are six ways to do that. And once we have made that choice, then we can independently either dress Bosco not at all (1 choice), in sweater alone (2 choices now), or in bow alone (1 choice). This provides for [latex]6\times 4 = 24[/latex] possibilities, and reversing the roles of Amber and Bosco gives 24 more. Then, if we want both cats to wear sweater and bow, we have six choices of how to dress the first cat and two independent choices for the second — giving 12 more possibilities.  This accounts for the remaining 60 “pathwise matchings” to complete our set of 91.

This recursive thinking seems like it has potential to bootstrap from the general bipartite case to the tripartite case, and if so, perhaps also beyond to the k-partite case. I don’t have those details worked out just yet, though. Maybe there’s a more clever approach that I’m missing?

The Shrinking Problem

Even more interesting to me than the question about how to add new articles of clothing to this photoshoot is the question of how to incorporate some indistinguishability. For example, suppose in the original two-cats, two-sweaters problem I have two identical red sweaters. Then there are only four photographs possible: Both cats undressed, Amber wearing red, Bosco wearing red, and both cats wearing red.

Worse yet, what if my two cats were also identical twins? Then, there are three possible photographs, enumerated by how many cats are wearing a sweater in them: zero, one, or two.

If it weren’t for the no-replacement feature of this counting problem, there’d be no difference between having one red sweater or having two. Alas, the effect doesn’t lend itself to a simple quotient.

In the fancier cats/sweaters/bows example above, consider the effect of making two of the sweaters identical – say, two red sweaters and one green. Of the 91 path-matchings we counted previously, some of them had both the red and yellow sweaters sitting unmatched. In fact, this number is 21, being [latex]7 = Z(K_{2,2})[/latex] in which no sweater was worn, another 7 in which Amber wears the green sweater, and another 7 in which Bosco wears the green sweater. These 21 photographs are insensitive to whether the two other sweaters are the same color or different — they’re not being matched up with a cat or a bow anyway. So they are in bijection with the photographs in the red/red/green case in which both red sweaters are unmatched.

But the remaining 70 original path-matchings either involve the red sweater, the yellow sweater, or both. After the distinction between red and yellow is removed, there is now a [latex]2 = |S_2|[/latex]-to-1 correspondence from these red/yellow/green photos to the red/red/green photos. The action of the transposition exchanges the class of red-only photos with the class of yellow-only photos, and since the cats and bows remain distinguishable, also acts freely on the class of photos that matched both red and yellow sweaters. So adding this indistinguishability reduces the original 70 photos in this group to only 35.

In total, then, we arrive at [latex]21+35=56[/latex] possible photos when two of my sweaters have the same color.

How exactly to generalize this counting process, I have no idea. It feels like the worst kind of balls-and-urns type of problem: distinguishable urns, but partially distinguishable balls. What happens to my approach when multiple urns have some indistinguishable balls in them? What about multiple kinds of indistinguishability in the same urn (three identical red sweaters, three identical green sweaters, and two identical yellow ones)?

Feedback I’m looking for

I’ve stared at this problem for long enough on my sabbatical to convince myself that it’s probably not trivial. But beyond the results on Hosoya indices and Laguerre polynomials that were valid in the (fully distinguishable) bipartite case, I haven’t found anyone who’s either made the leap from bipartite edge-counting to k-partite path counting, or looked at the question of making some vertices in a partite part interchangeable.

But I’m also not a specialist in graph theory or combinatorics. Am I even approaching this question in a helpful manner? Are there better ways of reframing this type of problem that could be susceptible to a smarter attack?