Guiding questions:

1. Knots: What do you notice? What do you wonder?
2. Devise three ways to represent your knot, at least one of which is not a diagram.
3. Make a conjecture: could your representation determine a different knot? What does “different” even mean?
4. Make a conjecture: Is your knot knotted, or not knotted?
5. In what ways do you imagine knots can be mathematical objects?

Videos from class:

Homework and next steps:

1. Create your blog (WordPress, Blogspot, or Weebly are some options) and e-mail a link to Dr. Salomone.
2. Write a blog post of 500+ words on the following prompt. In your experience (as a teacher and/or a learner of mathematics), what does "algebraic thinking" typically mean for you? How is it similar to or different from other forms of mathematical reasoning? Where do you and your students most use algebraic thinking? What else do you imagine it can mean?
3. Test the following conjecture:

Guiding questions:

1. What is a rational tangle?
2. How are the operations of tangles (twist \(T\) and rotation \(R\)) related? How is each inverted?
3. What operations on rational numbers satisfy the same relations as the generators of the tangle group?
4. How can answering the previous question determine a numerical invariant for rational tangles?

Videos from class:

Homework and next steps:

1. Continuing Conjecture 2.0.2: Is there an example of a knot diagram with equal number of over crossing and under crossings whose knot is not amphichiral?
2. Blog (500-ish words): Today's activity was adapted from an activity written by James Tanton for use in a professional development session for middle-school math teachers. Reflect on today's activity in light of your own experiences with teacher professional development. Compare and contrast its approach with workshops you've participated in in the past. What would you say has typically worked well for you in PD workshops (and why)? What do you wish your PD workshops did more of / less of / differently (and why)?
3. Read: Tanton, sections 2-3 (pp. 14-23).

Guiding questions:

1. How do you compute the tangle number for a rational tangle?
2. To what tangle operations does addition/subtraction/multiplication of rational numbers correspond?
3. How do continued fractions help relate rational numbers back to rational tangles?

Videos from class:

Homework and next steps:

1. Sketch the rational tangles \(T_1,T_2,T_3\) whose tangle numbers (fractions) are \(F(T_1)=4/5\text{,}\) \(F(T_2)=-5/8\text{,}\) and \(F(T_3)=9/2\text{.}\)
2. The numerator of a rational tangle is defined as the knot (or link) obtained by joining the top endpoints and joining the bottom endpoints: 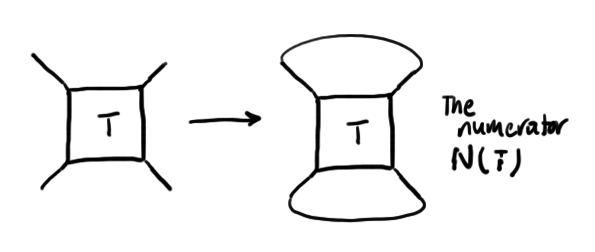Refer to the knots in Adams' table of knots and links. Find a rational tangle \(T\) whose numerator is the trefoil knot \(3_1\text{.}\) Repeat for \(4_1\) and \(6_2\) and \(8_4\text{.}\)
3. Compute the tangle number of each of the tangles you found in the previous exercise.
4. Blog (500-ish words): Today's results are written up nicely in two places: Tanton's notes (here) and the 2004 paper by Kauffman and Lambropoulou (here). Find one specific result (lemma or theorem) that both papers have in commmon. Compare and contrast the two authors' approaches to this result. As a reader, what do you think are the advantages and disadvantages to each paper's presentation of this content? How do you think the audiences for these papers are similar/different?
5. Read: Adams, 2.1 - 2.3 (pp. 31-51).

Guiding questions:

1. Does tangle number give us an invariant for (rational) knots? Why or why not?
2. How does Conway notation use the answer to #1 as a way to tabulate rational knots?
3. What are some advantages and limitations to Dowker's notation for knots, especially as compared with Conway's?

Videos from class:

Conjectures from today's class:

Homework and next steps:

1. Prepare a writeup of all exercises at the ends of Section 1.2 and Section 1.3. Most of these problems were also assigned in previous class meetings. If you can, do so on blank, unlined paper.
2. Project introduction: Read Angie Hodge's introduction to Math Teachers' Circles from the Math Ed Matters blog. Try to think of one or two "good Math Teachers' Circle problems," as she describes them, that relate to our material in algebra and knot theory. Briefly explain why the problem(s) you selected meet her brainstormed list of criteria. For inspiration, several examples of active Math Teachers' Circle activities for a variety of topics can be found on the Math Teachers' Circle Network site.
3. Blog (500-ish words): Download and listen to the February 7, 2018 episode of the My Favorite Theorem podcast by Dr. Kevin Knutson. In it, he has a conversation with knot theorist Dr. Candice Price about Conway's theorem on rational tangles that has driven the first three weeks of our course. In your blog, respond to their discussion. What new aspect(s) of knots/tangles did you pick up from listening? What question(s) did the interview raise for you, that you would ask her about? Any ideas for ways we could follow up on this conversation as a class?

Guiding questions:

1. How do the unknotting number, bridge number, and crossing number represent important features of knots?
2. What relationships between classes of knots are suggested by these invariants? What's been proven, and what remains an open question?
3. What examples show that each of these is not a complete invariant for knots?
4. What does it mean to \(k\)-color a knot? A rational tangle? How can 3-colorability be encoded in an equation that holds at each crossing?

Videos from class:

Homework and next steps:

1. Make a conjecture about how the following sentence may be completed: The Conway notation describes a knot whenever... and a link whenever... How might you approach proving your claim?
2. Determine the unknotting number and bridge number of the knot \(8_5\text{.}\) Since this knot is in the catalog, we believe it is a prime knot --- what else can we say about it on the basis of these invariants?
3. We saw in class that \(6_1\) is three-colorable. How many different 3-colorations exist for this knot? How do you know? If you label the arcs with colors \(x_1,x_2,\ldots,x_6\text{,}\) what system of equations would these numbers have to satisfy?

4. Blog (500-ish words): (1) Review the class's proposals for "good" Math Teachers' Circle problems for a knots and algebraic thinking workshop (problems with a low floor and a high ceiling). Other than your own, which problem would you select for a workshop and why? (2) Search the Math Twitter Blog-o-Sphere (#MTBoS) for a post in which teachers discuss either some aspect of knot theory specifically, or algebraic reasoning/algebraic thinking more generally. Review the post on your blog, and describe what you think it can tell us about what in-service teachers might be looking for out of a workshop on algebra and knot theory like ours.

   Search #MTBoS on Twitter. (Try adding more search terms as well.)

   Browse MTBoS resources on MTBoS.org.

Guiding questions:

1. How do colorability questions about knots become questions about linear algebra?
2. How do we do linear algebra with modular arithmetic, both by hand and using technology?
3. How can numbers of \(k\)-colorations be counted and used to distinguish among knots?

Sage cell for tricoloration of \(6_2\) from today's class:

M = MatrixSpace(IntegerModRing(3),6,6)
A = M([1,1,0,0,1,0 , 0,1,0,1,1,0 , 0,0,0,1,1,1 , 1,0,1,1,0,0 , 1,0,1,0,0,1 , 0,1,1,0,0,1])
print(A); print('\n'); A.echelon_form();

Videos from class:

Homework and next steps:

1. We saw in class on 2/26 that the knot \(6_2\) is: (a) ...not 3-colorable. (b) ...but it is 4-colorable. Use linear algebra to verify both conclusions. How many distinct, nontrivial 4-colorations are there for this knot, according to your results?
2. Refer to the two equivalent tangles from Exercise 1.2.4.2, which Adams notates as \begin{equation*} T_1 = -2\; 3\; 2 = \bigl[ [2], [3], [-2] \bigr] \qquad {\rm and} \qquad T_2 = 3\; -2 \; 3 = \bigl[ [3], [-2], [3] \bigr]. \end{equation*} Sketch an integer coloration for each tangle, and use each to compute the tangle numbers of \(T_1\) and \(T_2\text{.}\)

3. Blog (500-ish words): (1) My Favorite Theorem has featured another knot theory result this week! Listen to the March 7, 2018 episode with Laura Taalman and respond: what does this theorem tell you about why and how knot theory is interesting/challenging/valuable? What should it tell your students and colleagues about the nature of mathematics and mathematical reasoning? (2) At the midway point of this semester, how do you feel your own understanding of knots and algebra has evolved? What's worked best for your learning so far, and what has been most challenging (apart, perhaps, from drawing the darn diagrams)?

Guiding questions:

1. How do we test for \(k\)-colorability of knots when \(k \gt 3\text{?}\)
2. What linear algebra would be necessary to test for all possibility colorability options for a knot?
3. What is an oriented knot? Why is it important to orient a knot, and how can we distinguish positive crossings from negative?
4. How is the Alexander polynomial for a knot computed from a presentation matrix for its Alexander module?
5. What is a quandle, and what does it have to do with the crossings and colorations in a knot diagram?

Sage cell for computing the Alexander polynomial of the figure-eight knot \(4_1\) from March 26th's class. Note that the notation [0:3,0:3] says "take the three columns starting from the first (0th) and the three rows starting from the first (0th)", i.e. the top-right \(3\times 3\) submatrix. Try playing around with this to find other \(3\times 3\) (and \(2\times 2\)) subdeterminants!

Videos from class:

Homework and next steps:

1. Use a presentation matrix for the figure-eight knot \(4_1\) to determine its Alexander polynomial. For fun, repeat the process with a different \(3\times 3\) minor of the matrix; how does this change your process? Your answer?
2. Sketch a diagram of the trefoil knot \(3_1\text{,}\) and then apply a Type-I Reidemeister move to add a new crossing. Now, repeat the previous problem with this new knot diagram. What do you observe about the Alexander polynomial of this knot diagram?
3. Complete the verifications begun at the end of class (final video above) that each of the following defines a quandle: (a) A ring with unity \(S\) together with, for a fixed invertible element \(t\text{,}\) the operation \begin{equation*} x \triangleright y = t\, x + (1-t)\, y \end{equation*} and (b) A group \(G\) together with the operation \begin{equation*} x\triangleright y = y^{-1}xy. \end{equation*}

Guiding questions:

1. Why did we insist on using oriented knots to understand the fundamental quandle? What changes when the orientation is forgotten?
2. Other than the coloring data we obtain from realizing the fundamental quandle as an Alexander module, what other algebraic structures can reflect the properties of the fundamental quandle?
3. What is a homotopy group. and how is a homotopy group associated with a knot?

Videos from class:

Visualize a homotopy of two curves: click below to interact.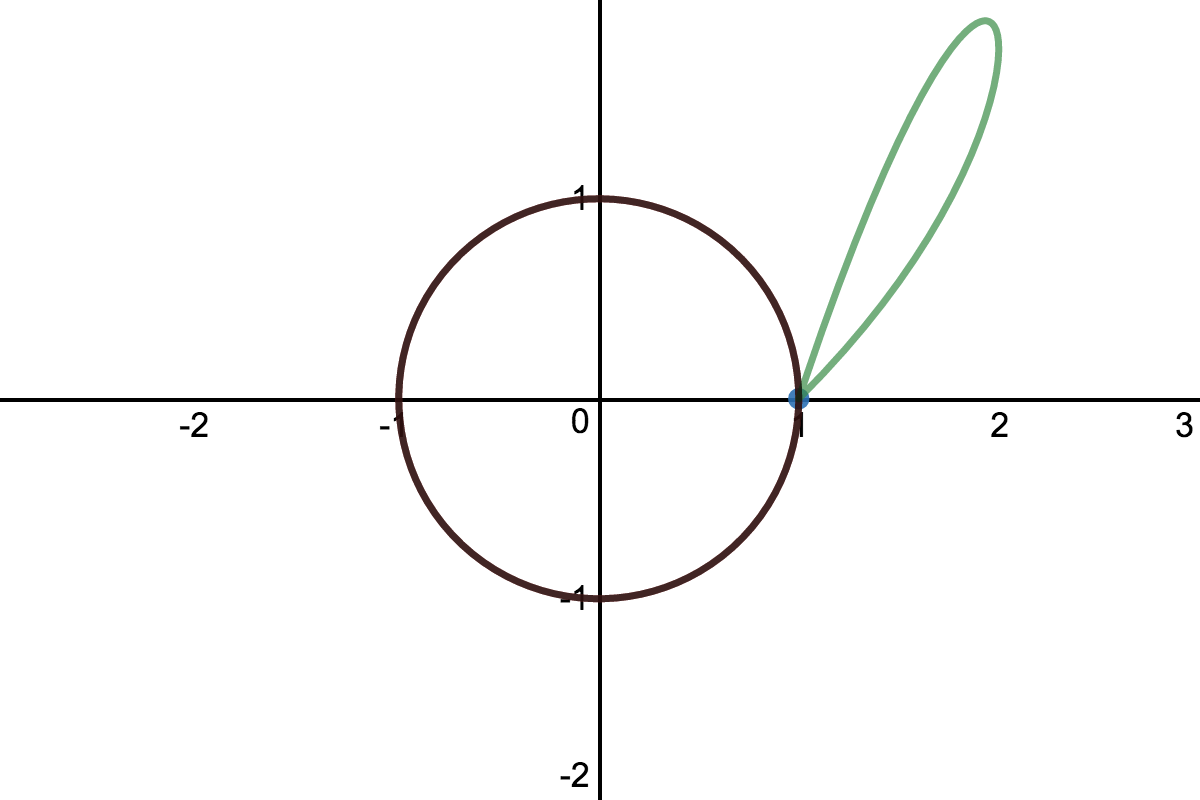

Homework and next steps:

1. Following the trefoil example from class, determine the full set of elements in the fundamental kei \(\mathcal{K}(4_1)\) of the figure-eight knot, and a table of operations for this kei. (Note that unlike the trefoil, not all elements of this kei will be arcs in the knot diagram.)
2. Refer to the homotopy of two curves in the interactive example above, which illustrates that the parametric curves \begin{equation*} {\bf r}_1(t) = \bigl( \cos 2\pi t, \sin 2\pi t \bigr) \end{equation*} \begin{equation*} \text{and}\qquad {\bf r_2}(t) = \bigl(1+4t-4t^2, 4t-4t^4 \bigr) \end{equation*} are homotopy equivalent. Would they still be homotopy equivalent if considered as curves in the punctured plane \(P = {\mathbb R}^2 \setminus \{(0,0)\}\text{?}\) Why or why not?
3. Consider the two parametric curves \begin{equation*} {\bf r}_2(t) = \bigl( \cos 2\pi t, \sin 2\pi t, \sin 2\pi t \bigr) \end{equation*} and \begin{equation*} {\bf r}_3(t) = \bigl( \cos 4\pi t, \sin 4\pi t, \sin 4\pi t \bigr). \end{equation*} Both are loops based at \({\bf x}_0 = \bigl(1,0,0\bigr)\text{.}\) (a) As \(t\) ranges from 0 to 1, how many times does \({\bf r}_2\) wind around the \(z\)-axis? What about \({\bf r}_3\text{?}\) (b) True or false, and explain: The function \begin{equation*} {\bf R}(t,h) = \biggl( (1-h)\cos 2\pi t + h\cos 4\pi t, (1-h)\sin 2\pi t + h\sin 4\pi t, (1-h)\sin 2\pi t + h\sin 4\pi t \biggr) \end{equation*} is a homotopy between \({\bf r}_2\) and \({\bf r}_3\text{.}\)
4. Thinking about the definition of the knot group, make a conjecture and explain your reasoning: The knot group of the unknot is... (Hint: using the simplest diagram of the unknot is probably enough to get a good idea.)
5. Blog (500-ish words): We came to consensus in class today that we're going to design our end-of-semester workshop around the theme: A Colorful Tangle Dance. Review James Tanton's Rational Tangle Dance teachers' circle materials; what portions of his workshop could we adapt, and what would we need to add? How would you envision building a lesson plan for a 2-hour teachers' circle around our theme, and what portion(s) of that plan would you most like to take responsibility to develop?

Guiding questions:

1. What does it mean for two based loops to be homotopy equivalent?
2. What modifications to the \(xy\)-plane give rise to nontrivial fundamental groups, and how?

Videos from class:

Homework and next steps:

1. We'll do this Fundamental Group Sorter activity at our next class meeting.